Interval Scheduling
Input A set of intervals, ${1,2,...,n}$ with start time $s(i)$ and finish time $f(i)$.
Output The largest subset of compatible intervals. Compatible intervals are those that do not overlap in time, that is $f(i) \leq s(j)$ or $f(j) \leq s(i)$.
The algorithm will select an interval using a greedy rule, add it to the schedule and remove all other incompatible intervals.
As pseudocode this would be
I = set of intervals
A = {}
while I is not empty
select some i from I using the greedy rule
add i to A
delete all intervals from I which are incompatible with i
return A
Possible greedy rules for interval scheduling
-
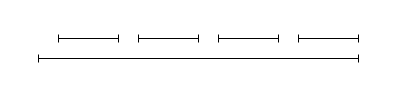
Earliest start time first - This is not optimal if the earliest interval has a long duration. In the example below, the longest interval is selected first, meaning only 1 interval can be scheduled whereas the optimal number is 4.
-
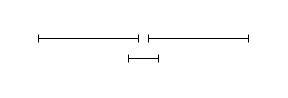
Shortest duration first - This is not optimal when the selected interval is incompatible with several longer, compatible intervals, as in the example below.
-
Fewest incompatibilities first - This seems like it might work but is not optimal for the example shown below.
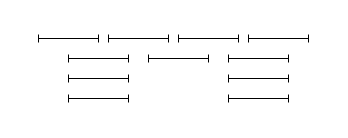
In this example, the middle interval would be selected first, eliminating the two above it. Then one from the left and one from the right would be selected, giving a schedule with 3 intervals. The optimal schedule would consist of the top row of intervals shown above and would have size 4.
-
Earliest finish time first - This rule is optimal.
Proof of optimality
Let $O$ be the optimal set of intervals and $A$ be the earliest finish time first output set. It is not possible to show $O = A$ as there may be several optimal sets for some inputs. Instead, it is shown that $A$ is optimal if $|A| = |O|$.
To prove this, it has to be shown that $A$ "stays ahead" of $O$. This means that some part of $A$ is always at least as good as some part of $O$.
Let $i_1,...,i_k$ be the intervals in $A$ in the order they were added to $A$. Let $j_1, ..., j_m$ be the intervals in the optimal solution $O$. $A$ is optimal if $k = m$. Assume the intervals in $O$ are ordered.
The greedy rule guarantees that $f(i_1) \leq f(j_1)$. It needs to be shown that for each $r \geq 1$ the $r^{th}$ interval in $A$ finishes no later than the $r^{th}$ interval in $O$.
Consider "For all indices $r \leq k$ we have $f(i_r) \leq f(j_r)$". This can be proven by induction. For $r=1$ the statement is true, as the algorithm starts by selecting $i_1$ with the earliest finish time. Assume $f(i_{r-1}) \leq f(j_{r-1})$. Since $O$ consists of compatible intervals, $f(j_{r-1}) \leq s(j_r)$. Combining this with the inductive hypothesis gives $f(i_{r-1}) \leq s(j_r)$. This means the interval $j_r$ was available when the greedy algorithm chose $i_r$, so $f(i_r) \leq f(j_r)$. $\blacksquare$
This shows that the greedy algorithm stays ahead, it can then be shown $k = m$ by contradiction. If $A$ is not optimal, an optimal set must have more intervals scheduled, that is $m > k$. Using the result of the last proof with $r = k$, $f(i_k) \leq f(j_k)$. Since $m > k$, there is a request $j_{k+1}$ in $O$. This request must end after $j_k$ ends and hence after $i_k$ ends. This means after deleting the set of intervals incompatible with $i_1,...,i_k$, the set of possible intervals $I$ still contains $j_{k+1}$. The greedy algorithm stops with request $i_k$ but it can only stop when $I$ is empty, a contradiction. $\blacksquare$
Complexity
Interval scheduling can be implemented more efficiently using the following algorithm:
sort I in order of finishing time
A = {I[1]}
for j in I
if s(j) > f(A[-1]) then
A += j
This has time complexity $O(n\log n)$ for sorting and $O(n)$ for iteration, giving overall $O(n\log n)$.