Merge Sort

Merge sort sorts a list by dividing it into two halves, sorting each half recursively and then merging the results in $O(n)$ time.

The runtime of merge sort can be represented using a recurrence: $$ T(n) = \begin{cases} O(1) & n \leq 2\\ 2T(n/2) + O(n) & \text{otherwise} \end{cases} $$ This is called the merge sort recurrence. If $n$ is a power of 2, it can be shown that $T(n) = O(n\log n)$.

Consider the recurrence tree:

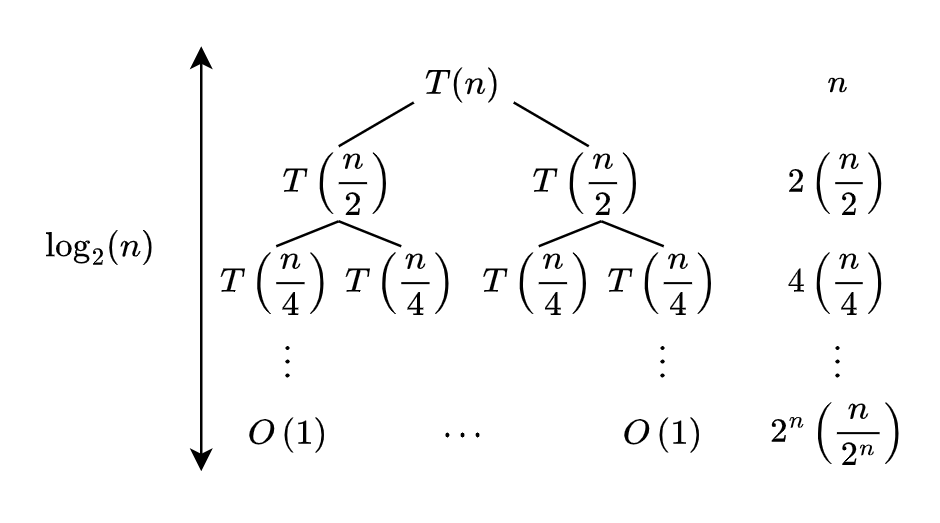
At each level $i$ there are $2^i$ recursive calls taking $T(\frac{n}{2^i})$ time plus the $O(\frac{n}{2^i})$ time to merge for each of the $2^i$ recursive calls, giving $O(n)$ additional work at each level. As the height of the tree is $\log_2(n)$, the overall runtime is $O(n\log_2 n)$ as there is $n$ time taken to merge for $\log_2(n)$ levels. As logarithms of different bases only differ by a constant, the time complexity of merge sort can then be simplified to $O(n \log n)$.