Finding the Closest Pair of Points

Input $n$ points of the form $(x_i, y_i)$

Output The closest pair of points by Euclidean distance

There is a trivial $O(n^2)$ algorithm for this problem which finds the distance between each pair of points.

min = null
for i in points:
    for j in points:
        if i != j and distance(i, j) < distance(min):
            min = (i, j)

There is a more efficient divide and conquer algorithm which can find the closest pair on $O(n\log n)$ time. This solution only considers points with distinct $x$- and $y$-coordinates for simplicity but can be extended to work for any points.

Consider the following:

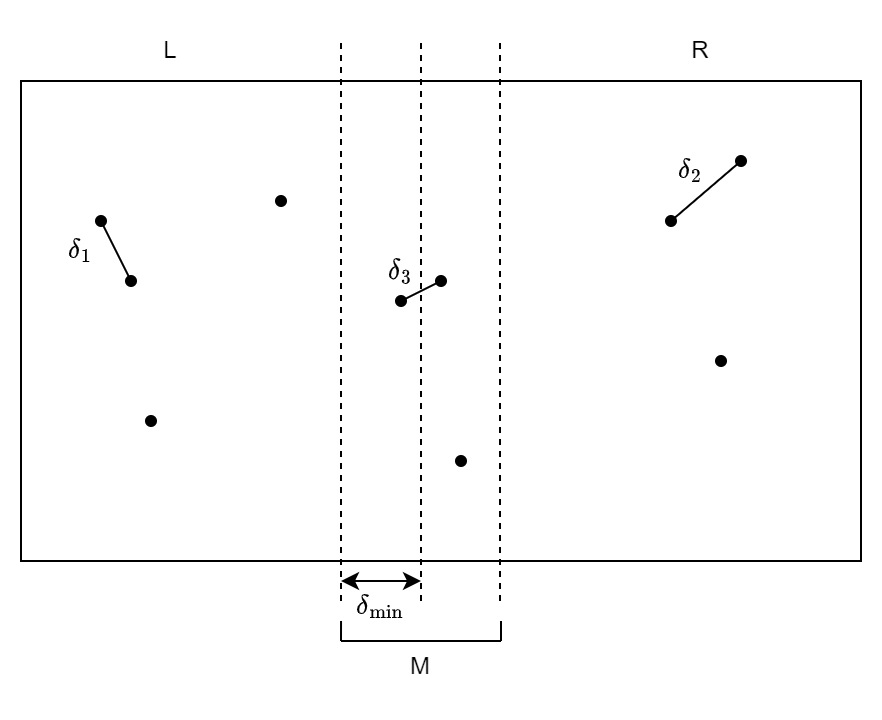
The points are sorted by $x$-coordinate and split into two groups, L and R.

• $\delta_1$ is the distance between the closest pair in L
• $\delta_2$ is the distance between the closest pair in R
• $\delta_3$ is the distance between the closest pair in M
• $\delta_{\min} = \min(\delta_1, \delta_2)$, which in the example above is $\delta_1$.

The closest pair is then given by $\min(\delta_1, \delta_2, \delta_3)$, which in the example above is $\delta_3$.

The region labelled M is the set of points from $L$ and $R$ which are closer to the centre than the closest pair in either half. This region needs to be considered in case the closest pair consists of a point from each side. Anything outside this region will be further apart than the closest pair in both halves so does not need to be considered.

The base case is when the size of a group is 2 or 3. The distances between all of the points can be calculated and the minimum returned.

The algorithm is as follows:

1. Sort points by $x$-coordinate
2. Split points into two groups of size $n/2$, labelled L and R
3. Recursively find the closest pair in each L and R
4. Find the closest pair in the region M
5. Return the closest of the three pairs from L, R and M.

Steps 1-3 and 5 are straightforward. Step 4 is not.

Consider the region M:

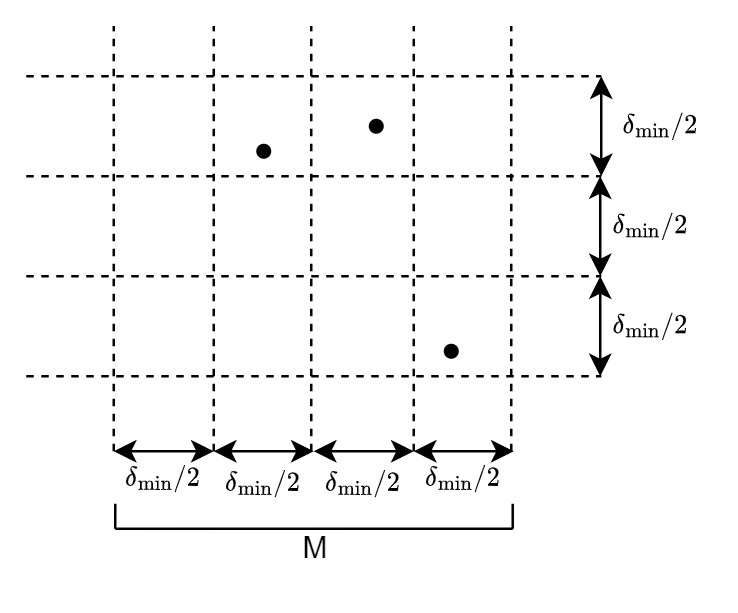
It can be divided into squares of size $\delta_{\min}/2$. There can only be one point in each square as otherwise $\delta_{\min}$ wouldn't be correct.

To find the closest pair, sort the points by $y$-coordinate ascending. The indices of any pair $(i, j)$ in the list where $\delta_{ij} < \delta_{\min}$ will differ by at most 7. I am not entirely sure why, but if they are more than 7 indices apart then their distance is greater than $\delta_{\min}$. For the example above there are only 3 points in M, so the minimum of the distances between them will be returned. If there were 16 points in M each point would only have to be compared to the next 7, not all remaining points.

Using this method, the algorithm is as follows:

1. Sort points by $x$-coordinate
2. Split points into two groups of size $n/2$, labelled L and R
3. Recursively find the closest pair in each L and R. Store the closest pair distance from both halves as $\delta_{\min}$
4. Consider points with $x$-coordinates within $\delta_{\min}$ of the centre line, label this set M
5. Sort the points in M by $y$-coordinate
6. Store an initial value of $\delta_3 = \delta_{\min}$
7. Compare distance of each point to the next 7, updating $\delta_3$ is a closer pair is found
8. Return the minimum of $\delta_{\min}$ and $\delta_3$

Complexity

The time complexity of finding the closest pair in M $O(n \log n)$ for the sorting and $O(7n) = O(n)$ for the distance comparisons. Given this, the recurrence is $$ T(n) \leq \begin{cases} O(1) & n \leq 3\\ 2T(\frac{n}{2})+O(n\log n) & \text{otherwise} \end{cases} $$ This means $n\log\left(\frac{n}{2^i}\right) = n\log(n) - n\log(2^i)=O(n\log n)$ is done at each level $i$ for a total of $\log_2(n)$ levels, giving an overall time complexity of $O(n\log^2(n))$.

It is possible to merge in $O(n)$ time by presorting the list by $y$-coordinate instead of sorting by $y$-coordinate for each iteration. Changing this in the recurrence above gives the merge sort recurrence. This results in $O(n\log n)$ time complexity overall.