Polynomial-time reductions
A polynomial time reduction from an algorithmic problem $X$ to another problem $Y$ is a polynomial algorithm for $X$ that uses $Y$, denoted $X \leq_p Y$. These calls to $Y$ are called oracle calls.
If $X \leq_p Y$ then
- There is a polynomial reduction from $X$ to $Y$
- $X$ can be reduced to $Y$
- $X$ is polynomial-time reducible to $Y$
- $Y$ is at least as hard as $X$
- If there is a polynomial time algorithm for $Y$ then there is a polynomial time algorithm for $X$
- If no polynomial-time algorithm exists for $X$ then no polynomial time algorithm exists for $Y$
Polynomial time reductions can be composed. If $X \leq_p Y$ and $Y \leq_p Z$ then $X \leq_p Z$.
For this module, reductions focus on decision problems. These are problems which can be answered with yes or no. For example, instead of "Find the shortest path from $u$ to $v$" a decision problem would be "Does there exists a path from $u$ to $v$ of length $k$?"
Independent set
An independent set of vertices is one in which no two vertices share an edge. More formally, an independent set is a set of vertices $S$ such that $S \subseteq V$ and $\forall v, w \in S$, $(v,w) \notin E$.
Consider the following graph
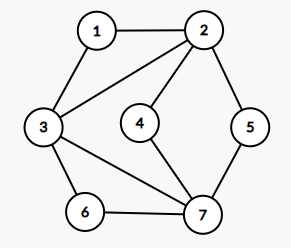
${3, 4, 5}$ is an independent set in the graph and ${1, 4, 5, 6}$ is the maximum independent set.
The independent set ($\text{IS}$) decision problem is as follows:
Input Undirected graph $G = (V, E)$ and a number $k$
Output Yes if $G$ has an independent set of size $k$, no otherwise
Vertex cover
A vertex cover is a set of vertices such that every edge is incident to some vertex in the set. More formally, a vertex cover is a set $S$ such that $S \subseteq V$ and $\forall (v,w) \in E$ either $v \in S$ or $w \in S$.
${1, 2, 6, 7}$ is a vertex cover in the graph above. ${2, 3, 7}$ is the minimum vertex cover.
The vertex cover ($\text{VC}$) decision problem is as follows:
Input Undirected graph $G = (V, E)$ and a number $k$
Output Yes if $G$ has a vertex cover of size $k$, no otherwise
Reductions
The largest independent set and smallest vertex cover partition the set of vertices. For the example above, ${1, 4, 5, 6} \cup {2, 3, 7} = V$.
$S$ is an independent set if $V \setminus S$ is a vertex cover.
Using this, independent set can be reduced to vertex cover in polynomial time, that is, $\text{IS} \leq_p \text{VC}$. The reduction is as follows:
$\text{IS}(G, k) = \text{VC}(G, |V| - k)$
This is a polynomial time reduction because
- it has polynomially many steps (in this case 1)
- makes oracle calls to $\text{VC}$
Vertex cover can also be reduced to independent set:
$\text{VC}(G, k) = \text{IS}(G, |V| - k)$
As the problems have been reduced in both directions, independent set and vertex cover are polynomially equivalent, denoted $\text{IS} \equiv_p \text{VC}$.
Set cover
A set cover of a set is a set of subsets which contain all items in the set. For example, ${1,2}, {3,4}$ would cover the set ${1,2,3,4}$.
The set cover ($\text{SC}$) decision problem is as follows:
Input Set of $U$ elements and a collection of subsets $S_1, S_2, ..., S_n \subseteq U$
Output Yes if there is a collection of subsets of size $k$ which cover the set, no otherwise
Vertex cover can be reduced to set cover. Let $I_v$ be the set of edges incident to a vertex $v$, that is, $I_v = {e \in E ;:; v \in e}$. The set cover of these edges of size $k$ is exactly the same as the vertex cover of size $k$, so the reduction is
$\text{VC}(G, k) = \text{SC}(E, {I_v ;:; v \in V}, k)$ where $G = (V, E)$.
Boolean satisfiability
A Boolean expression is satisfiable if there is some assignment of variables such that the expression evaluates to true.
The $\text{SAT}$ decision problem is as follows:
Input Boolean expression in conjunctive normal form (CNF) over a set of variables $x_1, ..., x_n$
Output Yes the expression is satisfiable, no otherwise
A CNF expression consists of a conjunction (and) of disjunctions (or), such as $(x_1 \vee x_2 \vee x_3) \wedge (x_4 \vee x_5) \wedge (\bar{x}_1 \vee \bar{x}_4)$.
A literal is a variable or its negation, such as $x_1$ and $\bar{x}_1$. A clause is a disjunction of literals, such as $(x_4 \vee x_5)$.
$\text{3-SAT}$ is a variation of $\text{SAT}$ with at most 3 literals per clause.
Consider the $\text{3-SAT}$ instance $(\bar{x}_1 \vee x_2 \vee x_3) \wedge (\bar{x}_2 \vee x_1 \vee x_3) \wedge (\bar{x}_1 \vee x_2 \vee x_4)$. $\text{3-SAT}$ can be reduced to $\text{IS}$ by producing a graph $G = (V, E)$ where $V$ is every literal occurrence ($x_1$ and $\bar{x}_1$ are distinct literal occurrences) and $E$ contains an edge between every literal in the same clause and between pairs of negated literal occurrences.
For example, the instance above becomes
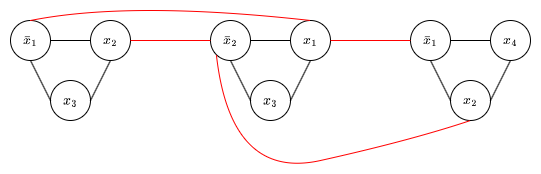
where the black edges are between literal occurrences in the same clause and red edges are between literal occurrences and their negations in different clauses.
Only one literal occurrence in each clause needs to be satisfied to satisfy the expression. A clause is represented by a triangle in the graph. That means there must be an independent set with one vertex in each triangle, so $\text{3-SAT}$ can be reduced to $\text{IS}$.
$\text{3-SAT}(\phi) = \text{IS}(G_\phi, k)$ where $G_\phi$ is the graph as obtained from the $\text{3-SAT}$ instance $\phi$ as above and $k$ is the number of clauses in $\phi$. Because the graph can be constructed in polynomial time, this is a polynomial time reduction. $\text{3-SAT} \leq_p \text{IS}$.