The Master Theorem

The master theorem states the solution of a recurrence of the form

$$T(n) \leq \begin{cases} O(1) & \text{if } n \leq b\\ aT(\frac{n}{b}) + O(n^c) & \text{otherwise}\\ \end{cases}$$

is given by

$$T(n) = \begin{cases} O(n^c) & c > \log_ba\\ O(n^{\log_ba}) & c < \log_ba\\ O(n^c\log n) & c = \log_ba \end{cases}$$

For example, the recurrence for merge sort is $T(n) \leq 2T(n/2) + O(n)$. This gives $a = 2$, $b = 2$ and $c = 1$ which then gives $log_ba = log_22 = 1$ and $c = 1$ so $c = \log_ba$. Therefore the solution to the recurrence by the master theorem is given by $O(n^1\log n) = O(n\log n)$.

Proof

Consider the recurrence tree:

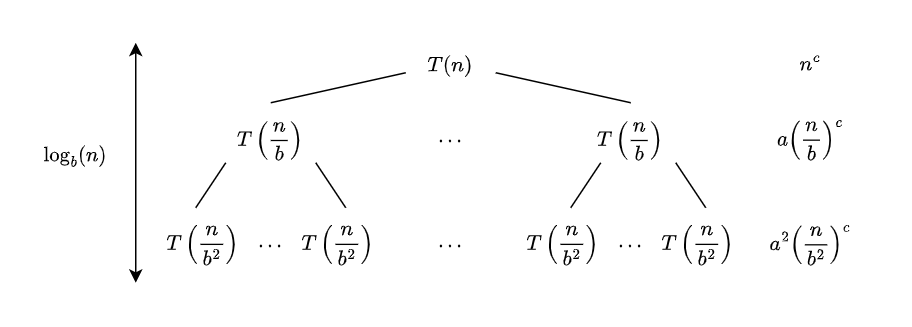
$T(n)$ has $a$ subtrees of size $\frac{n}{b}$, giving a complexity of $a\left(\frac{n}{b}\right)^c$ for the first level.

Each subtree in the first level has $a$ subtrees, giving a total of $a^2$ subtrees in the second level. Each of these contributes $\frac{n}{b^2}$ to the complexity, giving $a^2\left(\frac{n}{b^2}\right)^c$ for the second level.

From this, it can be seen that the complexity at level $i$ is given by $a^i\left(\frac{n}{b^i}\right)^c$, which can be rearranged to $\left(\frac{a}{b^c}\right)^i n^c$. The tree has height $\log_bn$, so the solution to the recurrence is given by $$ \begin{aligned} T(n) &\leq n^c \sum_{i=0}^{\log_bn}\left(\frac{a}{b^c}\right)^i\\ T(n) &= O\left(n^c \sum_{i=0}^{\log_bn}\left(\frac{a}{b^c}\right)^i\right) \end{aligned} $$

For case $c = \log_ba$

Rearranging $c = \log_ba$: $$ \begin{aligned} c &= \log_ba\\ log_b(b^c) &= \log_ba\\ b^c &= a \end{aligned} $$ Substituting this into the equation for $T(n)$ gives $$ T(n) = O\left(n^c \sum_{i=0}^{\log_bn}\left(1\right)^i\right) = O\left(n^c \left(\log_bn\right)\right) = O\left(n^c \log n\right) $$

For case $c > \log_ba$

Rearranging $c > \log_ba$ gives $a < b^c$. Because $\frac{a}{b^c} < 1$, the summation in $T(n)$ converges to a constant: $$ \sum_{i=0}^{\log_bn}\left(\frac{a}{b^c}\right)^i = O(1) $$ This gives $$ T(n) = O(n^c \times O(1)) = O(n^c) $$

For case $c < \log_ba$

Rearranging $c < \log_ba$ gives $b^c < a$, so $\frac{a}{b^c} > 1$. Using the sum of geometric series and some rules for logarithms, the summation can be expanded to $$ \begin{aligned} \sum_{i=0}^{\log_bn}\left(\frac{a}{b^c}\right)^i &= \frac{\frac{a}{b^c}^{1 + \log_bn}-1}{\frac{a}{b^c} - 1}\\ &= O\left(\frac{a}{b^c}^{1 + \log_bn}\right)\\ &= O\left(\frac{a}{b^c}\times \frac{a}{b^c}^{\log_bn}\right)\\ &= O\left(\frac{a}{b^c}^{\log_bn}\right)\\ &\text{using } x = y^{\log_yx} \text{:}\\ &= O\left(\frac{\left(b^{\log_ba}\right)^{\log_bn}}{\left(b^c\right)^{\log_bn}}\right)\\ &= O\left(\frac{\left(b^{\log_bn}\right)^{\log_ba}}{\left(b^{\log_bn}\right)^c}\right)\\ &= O\left(\frac{n^{\log_ba}}{n^c}\right) \end{aligned} $$ Therefore, $T(n)$ is given by $$ T(n) = O\left(n^c \times O\left(\frac{n^{\log_ba}}{n^c}\right)\right) = O\left(n^{\log_ba}\right) $$

Therefore all cases of the master theorem have been proven. $\blacksquare$